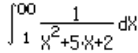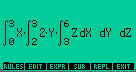By Carlos Marangon Jan, 20 1999
Reviwed dec 24, 2003
1-Definitions
1.1-Integral
Mathematical entity used to calculate area, volume, length,
centroids, etc.
An integral is applicable to a continuous function of an
interval on a definite variable of the function.
It is represented by the symbol 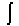 |
1.2-Definite Integral
| The expression represented by |
|
Definite integrals are used to calculate, in general, numeric values of areas, volumes, centroids, lengths, etc. It can be compared to the sum of all the elements of area of width dx and of height y=f(x) of a function plot . | ||
|
When dx tends to zero the number of elements tends to infinite and the sum more perfect, giving best precision to the calculation. We have so the " Summa Integrallis " of the function. An integral can be avalied summing all thiny elements of lenght dz and height y=f(x). The result of the operation is so much closer of the true value of the integral as minor is the dx , and consequently larger the number it of elements as well as the time taken to execute the calculation. In the illustration a and b are the limits of integration, the color lines are area elements, dx the lenght of the area elements and f(x) the height of the area element. |
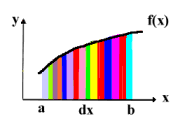 The summation of finite number x of elements of height y=f(x) and xx of width dx to avaliate the integral |
|
1.3-Indefinite Integral
|
The expression represented as |
| The calculus of an indefinite integral is basically to find another function called antiderivative, whose derivative results in the integrand f(x). |
|
It is usually called SYMBOLIC INTEGRAL, for HP48
users.
The expression symbolic integral is not current in
mathematical comunities, however.
| 1.4-Improper Integral name given to the expressions represented as |
2-Using HP48 to Solve Integrals
Note: check flags -01,-02 and -03 before try solve an integral.
They must be set
according to the result you wish, symbolic or numeric.
2.1-Indefinite integrals
HP48 is unable to solve all kinds of indefinite integrals.
Please, see page 20-8 of the Users's Guide for more information.
The screenshots below show the result for a function
it can't integrate and another function that it integrate.
 Integrate Solve Aplication |
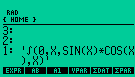 It just shows the expression of the integral if it doesn't solve. |
 Integrate Solve Aplication |
 It shows the result, like this, when it solves the integral. |
To solve an indefinite integral all we need is execute,
 |
|
| Enter the EXPR and VAR, LO and HI , set result as SYMBOLIC and press OK in the menu. |
|
| Note: You can also solve integrals using the EQUATION WRITER and pressing EVAL when finish writting the expression. |
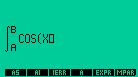 Writing the integral in the EQUATION WRITER |
2.2-Definite Integrals
HP48 G series can solve all the definite integrals and it takes
more or less time to solve according to the precision of the
calculus.
To solve a definite integral all you need is execute,
 |
|
| Enter the EXPR and VAR
, LO and HI , set result as NUMERIC and press OK in the menu. |
|
| Note: You can also solve integrals using the EQUATION WRITER and pressing EVAL when finish writing the expression. |
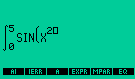 Writing the integral in the EQUATION WRITER |
| 2.3-Speeding the Numeric Integration HP48 G series permits speed the time of integration, in spense of the precision of the calculus. Defining the number of decimal digits it is possible to make the calculator solve integrals faster than when using the full 12 digits value. To speed the calculation it is needed define the number of decimal digits using the function FIX. It can be set usually 3 FIX, 5 FIX or 8 FIX according to the precision. |
 Number format screenshot |
2.4-Table of results of Calculations
|
Lets integrate f(X)=sin(X) on the variable X form 0 to 50 |
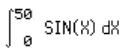 |
HP48 returns the following values according to the precision
and times to solve an integral.
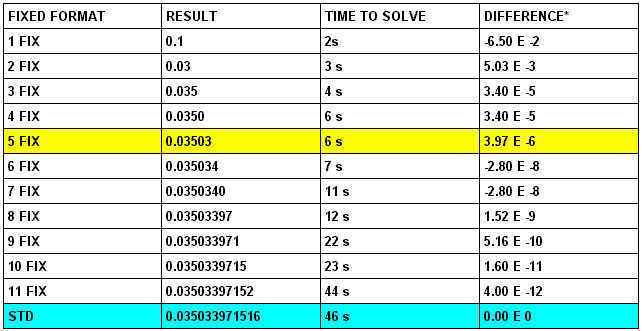
|
* The difference shown in the fourth column is the value we get
when subtract the result of the respective fixed format from the
value calculated with the HP48 working in the most precise mode ,
i.e. in the STD mode. As we can see in the yellow row, the result for HP48 working at the fixed format 5 FIX, is a good result. So we can conclude it is satisfactory use 5 FIX to solve numeric integrals. |
2.5-Improper Integrals
HP48 can solve improper integrals, but it needs a preliminar
variable replacement.
Be sure the improper integral converges before integrate, or it
will return an
absurd value and takes much time.
For example:
|
Lets integrate the function besides, on the variable X , from 1 to infinity |
|
A preliminary calculus is necessary in order to replace variables.
Lets use of an mathematical shotcut to replace the variable.
Lets make X = tan(Y) and calculate.
1- making X = tan(Y)
2- replacing dx for dy
dX/dY = d(tan(Y))/dY. It results dX = (1+ tan 2 (Y)) dY
3- replacing the function f(X) = f(tan(Y)) ;
for the function f(X)=1/(X 2 +5X+2) we have f(tan(Y)) = 1/( tan 2 (Y) + 5. tan(Y) +2)
4- replacing the limits
We have X=1 as lower limit and X=∞ as upper limit.
From the replacement formula we know that X=tan(Y)
so
1=tan(y), isolating Y we have Y=atan(1)
and
∞ =tan(y)
Isolating Y we have Y=atan(∞) ,
that in HP48 syntax can be written as Y=atan(MAXR)
Note:
If the limit is X= - ∞ it can be replaced by Y=atan(- MAXR).
Remember that in HP48 - ∞ is not MINR (1E-
499) neither -MINR (-1E-499).
These values are closest to zero, and not to - ∞.
To be accurate...

These replacements work for the greatest part of improper
integrals.
2.6-Replacing in the Formula
| Now we are able to replace the expressions in the formula | 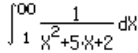 |
|
| 1 - Replacing the limits ∞ for atan(MAXR) and 1 for atan(1) |
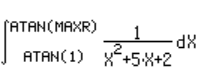 |
|
| 2 - Replacing f(x) for tan(x) | 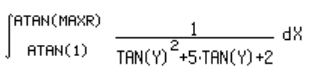 |
|
| 3 - Replacing dx for (1+tan(x) 2 ) | 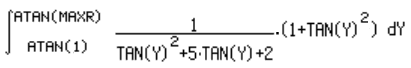 |
|
Try use the replacement expressions in the table above for more
examples of improper you have in your book of calculus integrals
and check the result.
Solving the Improper integral in the HP48G Series.
|
Now all we need is write the integral in the EQUATION WRITER |
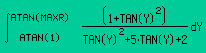 Long screenshot of the equation
|
| and press EVAL to get the result. |
|
2.7-Solving Double and Triple Integrals
The steps to solve double and triple integrals are not
difficult.
It is basically solve an integral 2 or 3 times.
All you need is write the expression in the EQUATION WRITER
 Writing a Double Integral |
|
and press EVAL to solve.
3-Exercises
Use HP48 and the methods explained in this document to solve the
following integrals:

4-Copyrights:
This document can be copied and freely distributed for
educational purpose.
It is prohibited its reproduction for non-educational purpose.
Sell this document as well use it for comercial purpose is not
permitted.
Exclude or modify the name of the author is not permitted.
If you sell it to a friend, please, sell it for a just price.
Publishing in sites is permitted since you don't modify this
document.
Use it in classes or for learning is freely permitted.
This document is CAREWARE
I will maintain this document at http://www.area48.com/integral