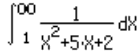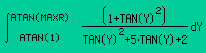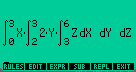Por Carlos Marangon Jan, 20 1999
Revisado em 24/12/2003
1-Definções
1.1-Integral
Elemento matemático usado para calcular área,
volume, comprimento, centroides, etc.
A integral é aplicável a uma função
contínua em um intervalo em uma variável definida da
função.
A integral é representada pelo
símbolo 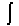 |
1.2- Integral Defiida
| A expressão representadas por |
|
Integrais definidas são usadas para calcular, em geral, valores numéricos de áreas, volumes, centroides, comprimentos, etc. Uma integral definida pode ser comparada com todos os elementos de área de comprimento dx e altura y=f(x) de um gráfico de uma função. Quando dx tende a zero o número de elementos de área tende ao infinito e a soma mais perfeita, dando melhor precisão ao cálculo. Temos então a "Summa Integrallis" da função. |
||
|
Uma integral pode ser avaliada somando-se todos os elementos de comprimento dx e altura y=f(x). O resultado da operação é tanto mais próximo do valor real da integral quanto menor for dx, e consequentemente maior for o número de elementos de área bem como o tempo necessário para calculá-la. Na figura ao lado a e b são os limites de integração, as linhas coloridas os elementos de área, dx o comprimento dos elementos de área e f(x) a altura dos elementos de área. |
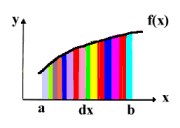 O somatório de um número finito de elementos de altura y=f(x) e comprimento dx para avaliar o valor da integral definida. |
|
1.3-Integral Indefinida
|
A expressão representada por |
| O cálculo de uma integral indefinida é basicamente encontrar uma outra função chamada antiderivada cuja derivada resulta no integrando f(x). |
A Derivada da
Antiderivada |
Muitas vezes a integrai indefinida é chamada
de INTEGRAL SIMBÓLICA, por usuários da HP48.
O termo integral simbólica não é tido como
termo corrente em comunidades matemáticas entretanto
| 1.4-Integral Imprópria Nome dado a expressão representada por |
2-Usando a HP48 para
resolver Integrais
Nota:
Verifique os flags -01,-02 e -03 antes de tentar resolver as
integrais.
Os flags devem estar definidos de acordo com o resultado
desejado, isto é,
numeric para numérico ou symbolic para
simbólico.
2.1-Integrais
Indefinidas
A HP48 é incapaz de resolver todas as
integrais indefinidas.
Veja a página 20-8 do Guia do Usuário (Users's Guide)
para
maiores informações.
As telas abaixo mostram uma função a HP48
integra
e outra que ela não integra, respectivamente.
 Aplicação Integrate Solve |
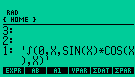 A HP48 mostra apenas a expressão da integral se não consegue resolvê-la |
 Aplicação Integrate Solve |
 A HP48 mostra um resultado, semelhante a este, se resolve a integral |
Para resolver uma integral definida só precisamos executar:
 |
|
| Entre com
EXPR e VAR, LO e HI, defina o resultado como SYMBOLIC e pressione OK no menu |
|
|
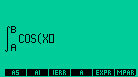 Escrevendo a integral no EQUATION WRITER |
2.2- Integral Definidas
As HP48 da Série G conseguem resolver
todas as integrais numéricas definidas
e demoram mais ou menos tempo de acordo com a precisão do
cálculo
Para resolver uma integral definida só precisamos executar
 |
|
| Entre com
EXPR e VAR, LO e HI, defina o resultado como NUMERIC
|
|
| Nota: Também é possível resolver integrais usando-se o EQUATION WRITER e pressionando-se EVAL quando se terminar de escrever a expressão. |
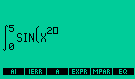 Writing the integral in the EQUATION WRITER |
| 2.3- Aumentando a
Velocidade da Integração Numérica
As HP48 da Série G permitem acelerar o tempo de
integração, às custas da precisão do
cálculo. Redefinindo-se o número de casas decimais
é possível fazer a calculadora resolver integrais
mais |
 |
| Para acelerar a velocidade de
cálculo de integrais é preciso redefinir o número
de casas decimais, usando a função FIX. Pode ser usado,
em geral, 3 FIX, 5 FIX ou 8 FIX de acordo com a precisão e o
tempo desejado.
|
2.4-Table of results of Calculations
| Integrando-se
f(X)=sin(X) sobre a variável X de 0 a 50 |
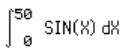 |
A HP48 retorna os seguintes resultados de acordo com a precisão
e o tempo necessário para resolver a integral
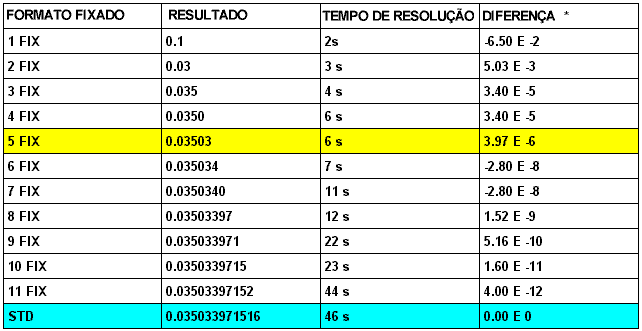
| A diferença mostrada na
Quarta coluna é o valor obtido quando subtrai-se o resultado
do respectivo formato fixado do valor calculado com a HP48 trabalhando no modo mais preciso, isto é, no modo STD. Nota-se na linha amarela que o resultado da
HP48 trabalhando com o formato fixado |
2.5-Integrais Impróprias
A HP48 é capaz de resolver integrais impróprias, mas
se faz necessário uma mudança de variável.
Certifique-se que a integral converge antes de executar a
integração, ou o resultado será absurdo e
demorará muito tempo.
Por exemplo:
|
Integrando-se a função
ao lado |
|
Um cálculo preliminar para
substituição de variável é
necessário.
Usa-se então um artifício matemático para
substituir a variável.
Faz-se X = tan(Y) e inicia-se o calculo.
1- fazendo-se X = tan(Y)
2- substituindo-se dx por dy
dX/dY = d(tan(Y))/dY resulta dX = (1+ tan2(Y)) dY
3- substituindo-se a função
f(X) = f(tan(Y)) ;
pela função f(X)=1/(X2+5X+2)
vem f(tan(Y)) = 1/(
tan2(Y) + 5. tan(Y) +2)
4-substituindo-se os limites de
integração
Tem-se X=1 como limite inferior e X=¥ como limite superior.
da fórmula de substituição sabe-se que
X=tan(Y)
1=tan(y), isolando-se Y vem Y=atan(1)
e
¥=tan(y), isolando-se Y vemY=atan(¥ ),
que em sintaxe de HP48 pode ser escrito como Y=atan(MAXR)
Nota:
Deve-se lembrar que na HP48 - ¥ não é MINR (1E- 499)nem -MINR (-1E-499).
Em suma:

Estas substituições
funcionam para grande parte das integrais
impróprias.
2.6-Substituindo na fórmula
| Já se pode substituir as expressões na fórmula. | 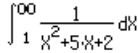 |
|
| 1-substituindo-se os limites ¥ poratan(MAXR) e 1 por atan(1) |
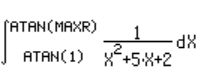 |
|
| 2-substituindo-se f(x) por tan(x) |
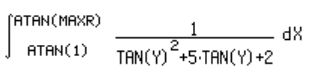 |
|
| 3-substituindo-se dx por (1+tan(x)2) |
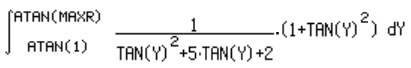 |
|
Tente usar estas as expressões de substituição da
tabela acima para mais exemplos
de integrais impróprias que se encontram em seu livro de
cálculo
Resolvendo Integrais Impróprias na HP48 Série G
|
Escreve-se a integral no |
|
| e pressiona-se EVAL para se obter o resultado. . |
|
2.7-Resolvendo Integrais Duplas e Triplas.
O procedimento para se resolver integrais duplas e tripas
é simples.
É basicamente resolver uma integral duas ou três
vezes.
Primeiro escreve-se a expressão no EQUATION WRITER
 Escreve-se uma Integral Dupla |
|
e pressione EVAL para se obter o resultado.
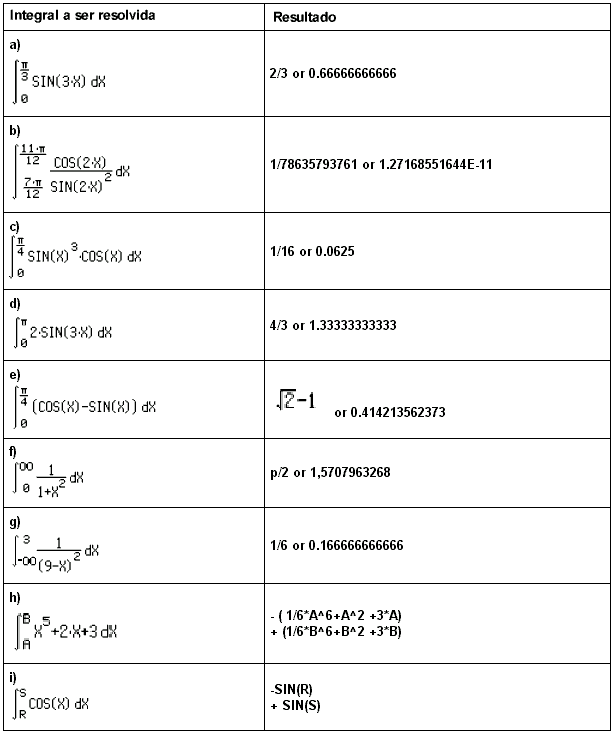
3-Exercícios
Use a HP48 e os métodos explicados neste documento para
resolver as seguintes integrais
4-Direitos Autorais
Este documento pode ser copiado e livremente distribuído
para fins educacionais. A reprodução deste documento
para fins não educacionais é proibida. Vender este
documento para visando lucros pessoais é proibido. Excluir
ou alterar o nome do autor não é permitido. Se este
documento for vendido para um amigo, deve ser vendido a
preço de custo. A publicação deste documentos em
sites da Internet é permitida desde que este documento
não seja modificado. O uso deste documento em salas de aula
para fins de aprendizado é permitido.
Este documento é CAREWARE
Este documento será mantido no endereço http://www.area48.com/integral