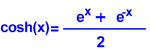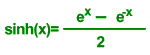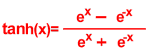Miscelânia
Miscelânia
Incluindo: Vetores, Funções Hiperbólicas, Números Complexos e Reais
Vetores
1) ABS
Calcula o módulo ou norma de um vetor
A norma do vetor [ a b c ] é definida como SQRT(a^2 + b^2 + c^2)
Exemplo:
Encontre a norma do vetor [2 3 4]
Nível 1: [2 3 4]
[MTH][VECTR][ABS]
Resultado: 5.38516480713
2) DOT
Calcula o produto escalar de dois vetores
O resultado é um número.
Exemplo:
[2 3 4].[6 7 8]
Nível 2: [2 3 4]
Nível 1: [6 7 8]
[MTH][VECTR][DOT]
Resultado: 65
3) CROSS
Calcula oproduto vetorial de dois vetores.
O resultado é um vetor.
Exemplo:
[2 3 4] x [6 7 8]
Nível 2: [2 3 4]
Nível 1:[6 7 8]
[MTH][VECTR][CROSS]
Resultado: [-4 8 -4]
4) 
V2
Converte os números dos níveis 1 e 2 em um vetor.
Exemplo:
Nível 2: 9
Nível 1: 8
[MTH][VECTR][
V2]
Resultado: [9 8]
5) V3
Converte os números dos níveis 1, 2 e 3 em um vetor.
Exemplo:
Nível 3: 4
Nível 2: 5
Nível 1: 8
[MTH][VECTR][V3]
Resultado: [4 5 8]
6) V
Converte um vetor em números da pilha operacional.
Exemplo:
Nível 1:[2 6 1 ]
[MTH][VECTR][V]
Resultado:
Nível 3: 2
Nível 2: 6
Nível 1: 1
Hyperbolic Functions
Funções Hiperbólicas são funções que tem por base o logaritmo
neperiano ou seja exp(x)
Para achar o valor de uma ffunções hiperbólica coloque o número na pilha
operacional
e pressione a respectiva função em [MTH][HYP]
Exemplo:
Calcular o sinh(5)
Nível 1: 5
[MTH][HYPER][SINH]
Resultado: 74.2032105778
Números Reais e Complexos
Na HP48/49 números complexos são representados entre ( ).
como ( parte reat, parte complexa)
Trabalhar com números complexos na HP48/49 é fácil.
Abaixo, estão listadas as funções mais úteis.
1) RE
Retorna a parte real de um número complexo
Exemplo:
Encontre a parte real de (123, 456)
Nível 1: (123, 456)
Pressione [MTH][NXT][CMPL][RE]
Resultado: 123
2) IM
Retorna a parte imaginária de um número complexo
Exemplo:
Encontre a parte imaginária de (123, 456)
Nível 1: (123, 456)
Pressione [MTH][NXT][CMPL][IM]
Resultado: 456
3) ABS
Retorna a norma de um númerocomplexo
Exemplo:
Encontre a norma do vetor (123, 456)
Nível 1: (123, 456)
Pressione [MTH][NXT][CMPL][ABS]
Resultado: 472.297575687
4) ARG
Retorna o valor do ângulo um número complexo
Exemplo:
Encontre o valor do ângulo de (123, 456)
Nível 1: (123, 456)
Pressione [MTH][NXT][CMPL][ARG]
Resultado:
74.9044791558 (modo ANGLE)
1.30732978576 (modo RAD)
5) CONJ
Rettorna o conjugado de um número complexo
Exemplo:
Encontre o conjugado de (123, 456)
Nível 1: (123, 456)
Pressione [MTH][NXT][CMPL][ARG]
Resultado: (123, -456)
xxxxxxxxxxxxxxxxxxPAREI AQUIxxxxxxxxxxxxxxxxxxxxxx
Números Reais
1) RND
Arredonda um número para o número de dígitos definido.
Nível 2:
1.8678987
Nível 1:
3
Pressione
[MTH][REAL][RDN]
Resultado: 1.868
2) TRNC
Trunca um número para o número de dígitos definido.
Nível 2:
1.8678987
Nível 1:
3
Pressione
[MTH][REAL][TRNC]
Resultado: 1.867
3) MOD
Retorna o resto da divisão de dois números
Exemplo:
Nível 2: 14
Nível 1:3
Pressione [MTH][REAL][MOD]
Resultado: 2
Nota: 8 / 3 = 4 e sobra 2.
4) IP
Mostra a parte inteira de um número
Exemplo:
Nível 2: 1.8678987
Pressione [MTH][REAL][IP]
Resultado: 1
5) FP
Mostra a parte fracionária de um número
Exemplo:
Nível 2: 1.8678987
Pressione [MTH][REAL][FP]
Resultado:. 8678987
6) DR
Converts graus para radianos
Exemplo:
Nível 2: 45
Pressione [MTH][REAL][DR]
Resultado: .785398163397
7) RD
Converte radianos para graus
Exemplo:
Nível 2: .785398163397
Exemplo:
Pressione [MTH][REAL][RD]
Resultado: 45
8) CEIL
Retorna o maior inteiro mais próximo de um número
Exemplo:
Nível 2: 1,45
Pressione [MTH][REAL][CEIL]
Resultado: 2
9) FLOOR
Retorna o menor inteiro mais próximo de um número
Exemplo:
Nível 2: 1,45
Pressione [MTH][REAL][FLOOR]
Resultado: 1
10) %
Retorna a porcentagem
Exemplo:
Nível 2: 100
Nível 1: 12,67
Press [MTH][REAL][%]
Resultado:12.67
Autovalores e Autovetores
1) EGV
O comando
EGV calcula os autovalores (
eigenvalues) e os
autovetores (
eigenvectors) de uma matriz.
Exemplo:
Calcular autovalores e os autovetores da matiz
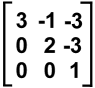Resolução:
1- escreva a matriz na HP48/49 como mostrado na figura abaixo:
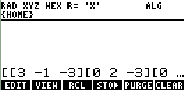
e pressione
[ENTER]
2- digite
EGV e pressione
[ENTER]
Vai aparecer:
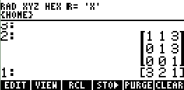
onde as colunas da matriz são os autovetores associados ao autovetor,
mostrado como um vetor, logo abaixo da matriz.
Neste exemplo:
[1 0 0] é o autovetor associado a
3
[1 1 0] é o autovetor associado a
2
[3 3 1] é o autovetor associado a
1
2) EGVL
O comando EGVL calculata o autovetor de uma matriz
Exemplo:
Calcular o autovalor da matriz
Resolução:
1- escreva a matriz na HP48/49 como mostrado na figura abaixo:
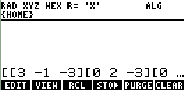
e pressione [ENTER]
2- digite EGVL e pressione [ENTER]
Vai aparecer um o vetorr
[ 3 2 1]
onde 3, 2 e 1 são os autovalores da matriz.
Nota:
Estes Exemplos foram feitos com a HP49 no modot RPN
A HP48 também é capaz de calcular autosvalores (eigenvalues) e autovetores (eigenvectors),
mas a HP48 mostra a matriz do autovetor em forma de linha, es autovalores
como um vetor.
Para os exemplos de EGV acima aparecerá algoparecido com,
[ [ 1 1 3 ] [ 0 1 3 ] [ 0 0 1] ]
[ 3 2 1].
Pressionando-se [SWAP] aparecerá.
[ 3 2 1]
[ [ 1 1 3 ]
[ 0 1 3 ]
[ 0 0 1 ] ]
Onde os autovetores são mostrados como colunas da matriz
e os autovalores como o vetor [ 3 2 1].
