Sistemas
Lineares
Resolvendo Um Sistema Linear
Dado o seguinte sistema linear:
ax + by = c
dx + ey = f
Para um sistema linear tem-se 2 matrizes como entrada de dados
1 - A matriz dos Coeficientes ou Matriz A
[ [a b] [d e] ]
2 - A matriz dos Termos Independentes, ou Matriz B
[ [ c ] [ f ] ]
Na HP48/49 as matrizes são escritas como:
[ [ row1] [row2]
[ row3] ....[rown]]
e para resolver o sistema linear pode-se seguir os passos abaixo:
Também é possível usar o Equation Writer para escrever matrizes
|
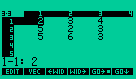
Escreva a matriz A |
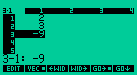
Escreva a matriz B |

e veja o resultado |
Resolvendo Um Sistema Linear de Números Complexos
| Resolve o sistema linear |
(5+j3)x + 7j y = 8
j6x + (7-j3) x = 3
|
 |
|
|
Na sintaxe da HP48/49 escreve-se:
(5,3) (0,7)
(0,6) (7,-3)
|

Pressione  e e 
para os dados na tela. |
|
|
Entre os dados dos termos
independentes e pressione
SOLVE, no menu.
|
 |
|
|
Pressione ENTER para ver
o resultado na pilha operacional.
Pressione  EDIT
para ver EDIT
para ver
melhor o resultado.
|
 |




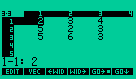
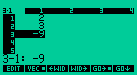


 e
e 


